競プロ覚書:深さ優先探索,幅優先探索 まとめ
基本的な全探索アルゴリズムである深さ優先探索,幅優先探索について,螺旋本を読んでまとめました.チートシートでは無いですが,この記事を見たら「なんとなく実装までいけそう」という記事を目指しました.「丁寧に一から解説」という記事ではないのでご注意ください.
この間の ABC119 の C 問題で,書けるようになった「つもり」の深さ優先探索を実装することができなかったので,猛省しながら書き上げました.
概要
DFS,BFS それぞれについて,
- アルゴリズムの概要
- 実装の大枠
を解説しています.
DFS に関しては,具体的な問題ではなく,実装のフレームワーク(のようなもの)に焦点を当てて解説しました(けんちょんさんの記事等を非常に参考にさせていただきました).これは,DFS は汎用性が広く,具体的な問題を解説するよりも有効だと考えたからです.
BFS に関しては,実装のフレームワークと AtCoder の問題による実例を示しました.BFS は問題で見かけることが少ないので(解いている問題が少ないのが原因),この機会に理解したことを記録しておこうという気持ちを込めて実例も加えました.
※ 記事中の,「計算量」は「時間計算量」を指します.
深さ優先探索
深さ優先探索(DFS: Depth First Search)は,状態の遷移が分岐するような処理を実装するのに有効です.過去のコンテストでは,
- 配列 A の要素 A[i] を端から「使う / 使わない」の処理(ABC119 - C)
- 文字集合があって任意の文字列を後ろに結合していく処理(ABC029 - C)
など,状態の遷移が分岐する処理(大事なことなので 2 回言いました)を実装するために使われました.DFS が最適解でなくとも,DFS で全探索を行うと解けるという問題は少なくないと思います.
アルゴリズムと計算量
根付き木での探索をイメージする方が多いと思います(「DFS は現在の深さと見てる要素を対応付けるのがコツ」というのを Twitter で見かけました).
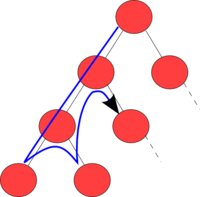
(Wikipedia より引用)
名前の通り,奥深くまで掘り下げていく探索アルゴリズムです.アルゴリズムは,上図を素直に辿った形になります.
- 根ノード root からスタート.
- 末端まで進めるまで進む.
- 末端に着いたら(進めなくなったら)一つ前に戻ってまだ進んでいない分岐を進む.
- 進んでいない分岐がなかったらもう一つ前に戻ってまだ進んでいない分岐を進む.(以下繰り返し)
「進めるだけ進んで止まったら戻って別の分岐へ」という手順となっています.最悪計算量は,全ての経路を考慮に入れるため,エッジの数 *1に比例し,
です.
大きなグラフに対する再帰を用いた DFS は,スタックオーバーフローを起こす可能性があるため注意が必要です. 程度までならスタック領域は不足しないです*2.
実装
DFS の 実装のフレームワークを示します.スタックと再帰による実装がありますが*3,ここでは再帰で実装します*4.実装は問題ごとに異なりますが,実装の大枠は大きく変わらないと思います.
int dfs(int pos, ~~~) { // 停止条件 // 深さに限らず,任意の停止条件を書く if (pos == N) return ~~~; // pos を進めながら(末端に進みながら)分岐処理 // 末端まで到達した時それぞれの分岐から値が返される // for 文で書ける場合は for 文で実装 int ret1 = dfs(pos + 1, 分岐 1); int ret2 = dfs(pos + 1, 分岐 2); int ret3 = dfs(pos + 1, 分岐 3); int ret4 = dfs(pos + 1, 分岐 4); ... // それぞれの分岐からの戻り値の処理を行う関数 return func(ret1, ret2, ret3, ret4); }
- 停止条件
- 分岐処理
の二つが大枠になります.他にも色々な書き方があると思いますが,自分が書きやすい,理解しやすい書き方が良いと思います.
問題
DFS を使って解ける問題です(DFS 以外の解法でも解けます).
- ABC029: C - Brute-force Attack
- ABC042: C - こだわり者いろはちゃん
- ABC114: C - 755
- ABC119: C - Synthetic Kadomatsu
幅優先探索
幅優先探索(BFS: Breadth First Search)は,「迷路の最短経路の探索」が最も直感的に分かりやすい例だと思います.近いところから万遍なく探索していくイメージです.
AtCoder に,迷路を題材にした BFS の教材的な問題があるのでそちらを参照することをお勧めします.アルゴリズム,実装のポイントを学べると思います.以下のリンクからどうぞ.
また,以下のサイトでは実際の迷路探索のシミュレーションを行うことができるので,お時間があれば参考にしてください.BFS に対するイメージが掴みやすくなります.
http://algoful.com/Archive/Algorithm/BFS
アルゴリズムと計算量
DFS は「深さを掘り下げていく」のに対し,BFS は「同じ深さのノードを調べて徐々に末端へ」というイメージです.
(よく分からない深さ優先探索より引用)
上図の数字は探索するノードの順番を示しています.それらの数字を見ると,「幅優先」という言葉通り同じ深さのノードを順に探索していくイメージが掴めると思います.アルゴリズムは,キュー queue を用いて実装します.
- 根ノードをキューに格納
- キューの先頭から要素を取り出し,
- ノードが探索対象であれば,探索をやめ結果を返す
- そうでなければ,現在のノードより一つ深いノード(子ノード)をキューに追加
- キューが空になったときに探索を終了する
以上のようなアルゴリズムとなっています.最悪計算量は DFS と同じく全ての経路を考慮にいれるため,エッジの数 に比例し,
です.また,
- 列挙が目的:深さが末端にたどり着いた時に終了
- 探索が目的:探索対象が見つかった時点で探索を終了
というように必要に応じて停止条件は書き分けるようにしてください.
実装
BFS のフレームワークと,迷路探索の実装例を示します.
フレームワーク
アルゴリズム通り,同じ深さのノード(状態)を探索していく.次のノード(状態)を順番に見ていき,条件を満たしたら一つ深いノード(下記の depth + 1 の部分)としてキューに格納する処理を書きます.以下,C++ で大枠を実装.
struct Object { // 任意の構造体 ll hoge; ... ll depth; } queue<int> q; Object start = {~~~, 0}; // 深さ 0 q.push(start); // 初期状態をキューに入れる int bfs() { while (!q.empty()) { // キューの先頭の要素を取り出す dequeue(pop) Object now = q.front(); q.pop(); // 停止条件 // if (now.hoge == target) return ~; // 探索対象 if (now.hoge == N) return ~; // BFS for (int i = 0; i < 次のノード(状態)の数; ++i) { Object next = {~~~, depth+1}; // 深さ(ステップ数)を一つ足す if (条件) { // 条件を満たしたら enqueue(push) // 問題により,同じ状態に戻らないようにする処理を書く(無限ループを防ぐ) q.push(next); } } } }
これをベースとすれば BFS が書けると思います.
BFS の実装例:迷路の探索
冒頭で紹介した AtCoder の問題で,BFS の実装例を示します.キューにどのように要素が格納され,取り出されるのかをイメージしながらご覧ください.コメントアウトとともにコードを上から読んでいけばなんとなく BFS が掴めるかと思います.
// ABC007_C #include <iostream> #include <string> #include <vector> #include <queue> using namespace std; using ll = long long; // 座標 corrdinate と深さを保持するための構造体 struct Corr { ll y; ll x; ll depth; }; ll N, M; // 迷路の縦,横 ll s_y, s_x, g_y, g_x; // スタート,ゴールの座標 ll y, x, depth; // キューから取り出した座標 vector<string> vec; // 座標を受け取る配列 queue<Corr> q; vector<ll> y_vec = {0, 0, -1, +1}; // 進む方向の簡便化,テクニックとして覚えておく. vector<ll> x_vec = {-1, +1, 0, 0}; // ループで回すことで上下左右に移動できるようになっている ll bfs() { while (!q.empty()) { Corr now = q.front(); q.pop(); // キューの先頭を取り出す y = now.y, x = now.x, depth = now.depth; // 行,列が y, x になっているので注意 // 停止条件:現在の座標がゴールなら深さを返す if (y == g_y && x == g_x) return depth; // 上下左右 4 方向を探索.進むことができればキューに格納する. for (ll i = 0; i < 4; ++i) { Corr next = {y + y_vec[i], x + x_vec[i], depth + 1}; if (0 <= next.y && next.y <= N-1 && 0 <= next.x && next.x <= M-1 && vec[next.y][next.x] == '.') { vec[next.y][next.x] = 'x'; // 同じ場所を探索しないようにする q.push(next); } } } return 0; } int main() { // input cin >> N >> M >> s_y >> s_x >> g_y >> g_x; s_y--, s_x--, g_y--, g_x--; // 0-origin にするため vec.resize(N); for (ll i = 0; i < N; ++i) cin >> vec[i]; // calculation Corr start = {s_y, s_x, 0}; // 初期位置の深さ(depth)は 0 q.emplace(start); // 初期位置をキューに格納 cout << bfs() << "\n"; return 0; }
問題
BFS に関する問題です.自分の解いた問題が少ないので列挙できませんでした.解いたら追加していこうと思います.
蛇足:再帰による DFS のイメージに関して思ったこと
蛇足です.再帰で実装した DFS に関して考えたことを雑に吐き出してみます.
再帰による DFS の自分の中では,「トップダウン」なイメージです.よーいどんで初期状態からスタートし, dfs という関数の中で勝手に分岐処理をしてくれるようなイメージ.一般的に知られている「末端までたどり着いたら戻って他の分岐へ」(バックトラック)というスタックが必要な処理を上手く(隠蔽しながら?)実装してくれてるなと思いました.
再帰関数の中で,分岐の部分が(以下のように)並んでいるとどうしても一斉にスタートしてるような気がしてしまいます(私だけかもしれませんが).
dfs(pos + 1, 分岐 1); dfs(pos + 1, 分岐 2); dfs(pos + 1, 分岐 3); dfs(pos + 1, 分岐 4); ...
しかし,コードが一行一行上から処理されていくことを考えると,一つの分岐に対して掘り下げて値を返しての繰り返しになっているため,結局バックトラックのような処理をしてるのかなとも考えました(スタックによる実装だと,各ノード(状態)の情報を保持しながら探索が進むので,一般的な DFS の感覚と実装の感覚が合います.).
思いついたままに書いてしまったので何を言ってるのかまとまりが付かなくなってしまいましたが,頭の中を少し整理するために考えを書いてみました.自分はこう考えているなどご意見があれば大変参考になりますので気軽にコメントいただけると嬉しいです.
終わりに
最後まで読んでくださりありがとうございました.感想,考え方の間違い,ご指摘等があれば,コメント,Twitter などでリプをいただけると幸いです.